Algoritmo para predecir el número de llamadas a emergencias
Uno de los algoritmos predictivos que hemos desarrollado dentro del proyecto SAPIENS es el que permite predecir el número de llamadas a un número de emergencias en función del día del año.
Dataset
Para este análisis hemos accedido a datos abiertos (Open Data) del Departamento de policía de la ciudad de Guelph (Ontario, Canadá) (accesible aquí). Descargamos 4 años de datos (2014 – 2017) en formato “.csv”. Cada dataset anual contiene aproximadamente entre 61.000 – 67.000 registros e información detallada sobre la llamada, entre las más importantes la fecha y hora, la dirección y la causa de la llamada.
Variables del dataset:
- OccurrenceNumber: ID del caso
- Address (a nivel de calle, n=1131)
- Reported Date (año-mes-día)
- Reported Time (HH:MM)
- Dispatch Type (N=227)
- Occurence Type (N=543)
- Dispatched (fecha y hora)
- Arrived
- Cleared
- Delay Time (duración; d:HH:MM:SS)
- Travel Time
- OnScene Time
- Response Time
Preparación y limpieza de datos
Una tarea imprescindible antes del propio análisis de datos es la limpieza y preparación previa. En nuestro caso, excluimos tanto los registros duplicados y como aquellos en los que faltaba información que era necesaria (por ejemplo, fecha y hora de la llamada). Para del año 2014 faltaban varias variables por lo que al final excluimos este año del análisis. Como resultado, el dataset contiene 191.225 registros de años 2015 – 2017.
En el siguiente paso creamos variables nuevas, basándonos en la fecha y hora de la llamada:
- hora de la llamada (0-23 h)
- día de la semana (lunes – domingo)
- número de la semana (1-52)
- mes (enero – diciembre)
- año calendario (2015-2017)
Por último, para la predicción de número de llamadas a nivel diario, creamos un nuevo dataset agregando el número de llamadas por día del calendario – este dataset contiene 1096 registros.
Análisis exploratorio
Antes de predecir el número de llamadas, centramos nuestra atención en el análisis exploratorio de los datos, enfocado al número de llamadas recibidas. En la figura 1 se resumen las siguientes observaciones:
- Existe una tendencia anual creciente
- El mes con más llamadas era septiembre y con menos febrero y diciembre
- El día de la semana con más llamadas era el viernes
- Se observa un patrón diario en el que aumentan las llamadas a partir de las 8h de la mañana, con el pico entre las 15h y las 16h de la tarde.

Figura 1: Resumen del análisis exploratorio del número de llamadas a emergencia entre años 2015 – 2017. Las líneas gris horizontales en el resumen por mes, día de la semana y hora del día indican valor promedio a lo largo de los 3 años.
En promedio, a lo largo de los 3 años analizados se recibieron:
- 5,300 llamadas por mes,
- 174 llamadas por día
- 7.3 llamadas por hora.
Por otro lado, exploramos también las causas de las llamadas más frecuentes (Figura 2):

Figura 2: Causas más frecuentes de las llamadas al número de emergencias de la ciudad de Guelph entre años 2015-2017.
Modelo predictivo
Construcción y evaluación del modelo
Para construir el modelo predictivo consideramos como variable dependiente el número de llamadas diarias y las siguientes variables independientes (input features):
- día de la semana,
- número de la semana,
- mes,
- año calendario.
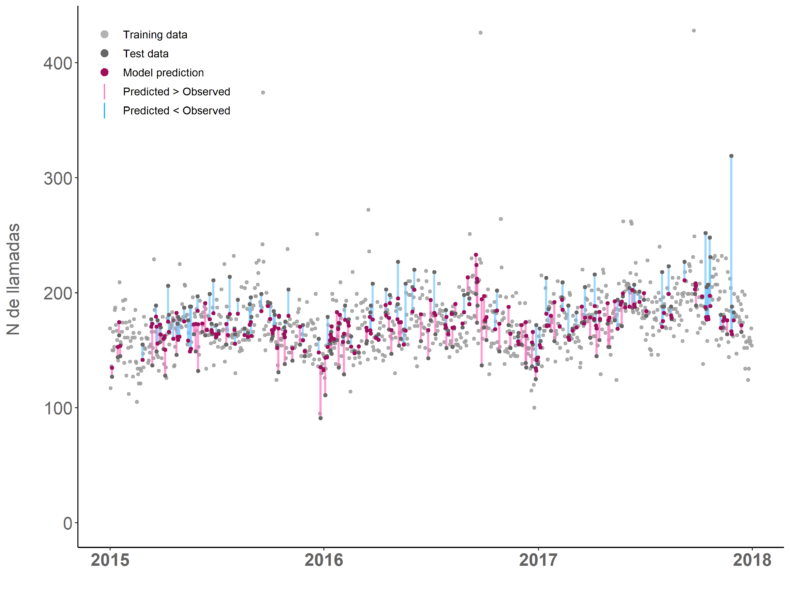
Dividimos el dataset aleatoriamente en training (80 % de datos) para entrenar el modelo y testing (20 %) para evaluar el modelo (Figura 3). Construimos varios modelos de regresión lineal múltiple combinando las variables independientes y seleccionamos el mejor modelo según el criterio de información de Akaike (AICc).
El resultado de este análisis nos indica que la mejor predicción se realiza teniendo en cuenta: el día de la semana, el número de semana y el año. Este modelo explica un 32 % de la varianza (valor de coeficiente de determinación R2=0,32).
Testamos el modelo aplicándolo al testing dataset. Para evaluar los resultados, exploramos los residuos del modelo: diferencia entre valores predichos y observados – la parte que el modelo no es capaz de explicar. Los residuos siguen una distribución normal que nos indica que el modelo se ajusta bien a los datos. También calculamos el error absoluto promedio del modelo (Mean Absolute Error), que es de 15,8 llamadas diarias (9 % del promedio de llamadas diarias).
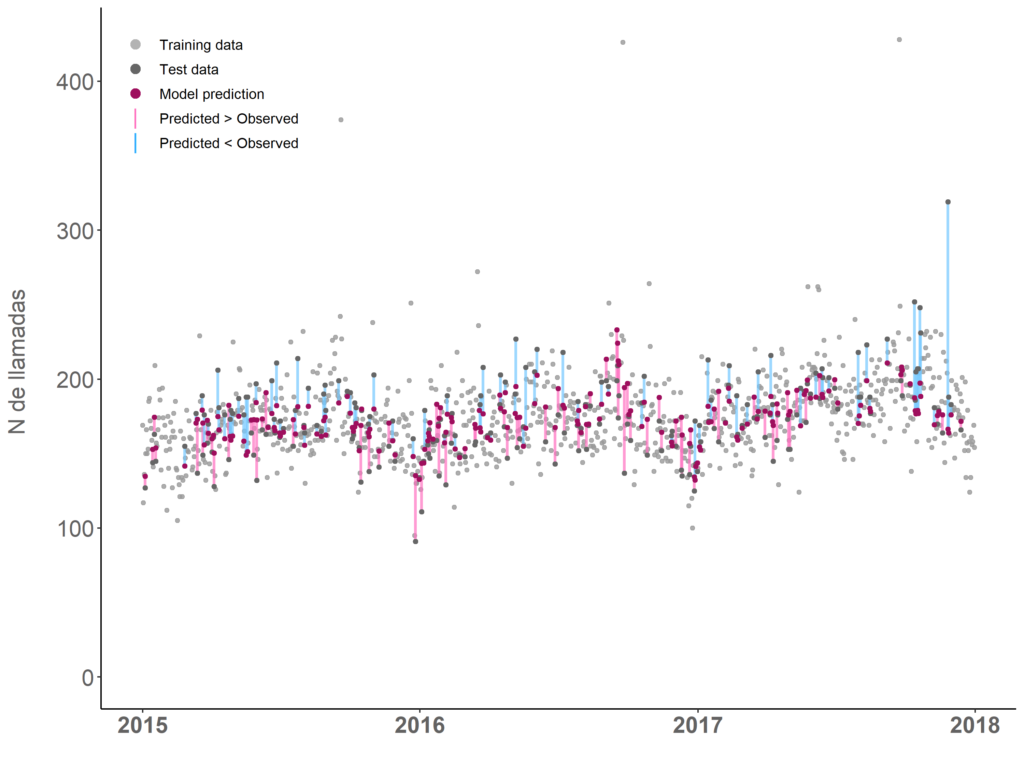
Figura 3: Training y testing dataset de modelo predictivo de número de llamadas por día calendario.
Predicción para el año 2018
Finalmente, aplicamos el modelo seleccionado a todo el dataset (2015-2017) para generar la predicción para el año 2018 (Figura 4). Vemos en gris los datos observados de los años 2015-2017 usados para construir el modelo, y en violeta la predicción. La línea violeta oscura indica los valores predichos, mientras que en color más transparente se representa el intervalo de predicción del 80 %. Según la predicción, por ejemplo el día 21/11/2018, siendo miércoles, semana 47 del año 2018, tenemos 80 % de confianza (probabilidad del 80 %) de que el número de llamadas estará entre 155 y 215, en promedio 185 llamadas para ese día.
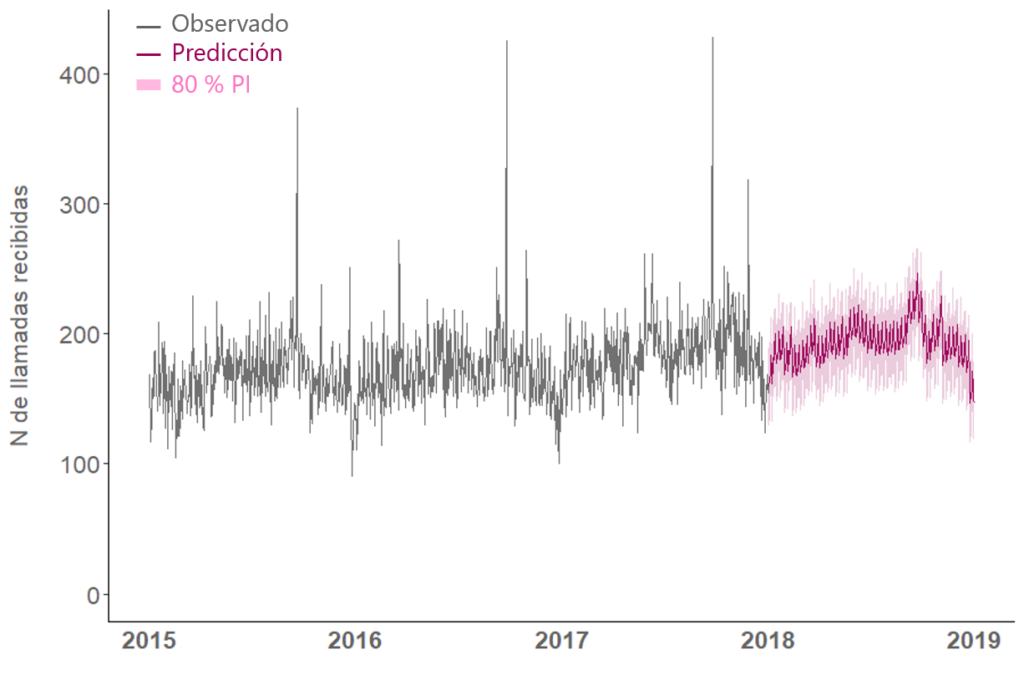
Figura 4: Predicción de número de llamadas para el año 2018 de la ciudad de Guelph.
Todo el análisis ha sido realizado en entorno R (R Core Team 2018) usando diferentes librerías (dplyr, ggplot2, cowplot, MuMIn).
Conclusiones
En este trabajo analizamos datos abiertos de llamadas a emergencia de la ciudad de Guelph. Construimos modelo predictivo para predecir número de llamadas diarias para el año 2018, basándonos en últimos tres años de datos, y consiguiendo una predicción con únicamente un 9% de error en el número de llamadas.
Nuestros resultados podrían servir para planificar número de operadores de emergencia disponibles y/o la cantidad de policías necesarios en la ciudad.
Por otro lado, el modelo es capaz, con tan sólo 3 variables extraídos de la fecha (día de la semana, número de semana, año calendario), explicar un 32 % de la varianza de la variable dependiente (número de llamadas). Esto sugiere que incluyendo información externa de otras fuentes de datos (por ejemplo datos meteorológicos, posición (latitud/longitud), fechas de ocurrencia de ciertos eventos, etc.) podríamos ampliar aún más la capacidad de predicción.
El proyecto SAPIENS está desarrollado con el soporte de:
![]()
Zuzana Zajková - author
4 Comentarios
Deja un comentario
Categorías
- Blog (6)
- Conocimiento (31)
- Gestión (17)
- Historias (24)
- Sectores (17)
- Adm. Pública (16)
- Tecnologías (3)
- Uso de Atlas SBI (5)
- Sectores (17)
- Machine Learning (5)
- LLM/GPT (3)
- Noticias (24)
- Proyectos (33)
- SAPIENS (12)
- SapiensXBot (4)
- Vídeos (20)
- General/Usuario (8)
- Técnico avanzado (5)
- Técnico Básico (7)

Hola,
Enhorabuena por tu post y trabajo.
Me gustaría saber si podria tener acceso al script/código de programación en R.
Gracias de antemano,
Saludos
Ivan,
Gracias por tu comentario. Siento no poder facilitarte el script, pero estaremos encantados en tener una reunión contigo y explicarte con más detalle el proyecto o comentar cualquier duda que puedas tener sobre cómo lo hemos enfocado (librerías, estrategia,…).
Saludos
consulta….felicitaciones por su trabajo…mi duda es…trataron a los datasets como series temporales o unieron los años en una sola base con una variables mes-año
Gracias por tu pregunta. En este caso, no tratamos el dataset como serie temporal, extrajimos de la fecha las variables: año, mes, número de la semana, día de la semana. El modelo (regresión lineal) lo construimos de la siguiente manera: el número de llamadas como variable dependiente y las variables mencionadas (año, mes, número de la semana, día de la semana) como variables independientes.
El dataset también se puede analizar como serie temporal (no está incluido en este blog), utilizando, por ejemplo, modelos ARIMA o prophet para construir modelo predictivo.
Saludos.